Das Ableiten von Funktionen gehört zur Differentialrechnung, wie der Fisch zum Wasser. Anhand der Differentialrechnung werden lokale Veränderungen von Funktionen untersucht, wie z.B. Nullstellen, Hoch-, Tief- und Wendepunkte, Sattelpunkt, Monotonie- und Krümmungsverhalten usw. All diese Eigenschaften von Funktionen werden im Rahmen der Kurvendiskussion untersucht, welche im letzten Teil der Artikelreihe „Differentialrechnung in 5 Schritten“ behandelt wird.

In diesem Artikel widmen wir uns zunächst dem Handwerkzeug der Differenzialrechnung, nämlich dem Bilden von Ableitungen. Neben einer kurzen Einführung zum Thema „Ableitungen“ und was das eigentlich genau ist, werden die wichtigsten Ableitungsregeln anhand von Beispielen betrachtet.

Ziel des dritten Teils „Ableitungsregeln Beispiele“ ist es, zunächst ein Verständnis für den Sinn und Zweck von Ableitungen zu schaffen. Und da in der Mathematik sehr unterschiedliche Funktionstypen existieren, bei denen entsprechend andere, bzw. Kombinationen mehrerer Ableitungsregeln angewendet werden müssen, sollen diese Ableitungsregeln anhand ausgewählter Beispiele anschaulich erklärt werden.

Ableiten von Funktionen: Was ist das und wozu ist das gut?

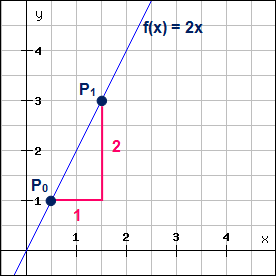
Anhand der Ableitung einer Funktion kann man ihre Steigung an einem bestimmten Punkt bestimmen. Wie im ersten Artikel „Einführung in die Differentialrechnung“ bereits erläutert wurde, verfügen nichtlineare Funktionen über mehrere Steigungen, je nachdem, wo genau man sich auf dem Funktionsgraphen befindet. Die Steigung einer linearen Funktion hingegen, z.B. 2x, ist recht simpel, schließlich handelt es sich dabei um eine Gerade, die überall die gleiche Steigung hat. Die Funktion 2x sagt nicht weiter aus, als das mit jedem zunehmenden x, der Funktionswert f(x), bzw. y um zwei Einheiten zunimmt. Bildlich kann man ein sogenanntes „Steigungsdreieck“ anlegen. Hierfür bestimmt man zwei Punkte auf der Geraden (P1 und P₀₎, verbindet diese durch Einzeichnen zweier Striche zu einem Dreieck und liest die Steigung dann anhand der beiden eingezeichneten Seiten ab:

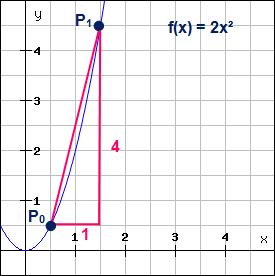
Doch wie sieht es z.B. bei der nichtlinearen Funktion 2x² aus? Hier haben wir es nicht mehr mit einer Gerade, sondern mit einer nach oben geöffneten Parabel zu tun. Wie hoch ist nun die Steigung der Parabel an der Stelle x₀=0,5? Zwar kann man sich der Steigung anhand eines Steigungsdreiecks nähern, allerdings erhält man aufgrund des gekrümmten Funktionsgraphen keinen exakten Wert für die Steigung an der Stelle x₀=0,5.

Um die exakte Steigung einer Funktion an verschiedenen x-Werten zu bestimmen, bedient man sich der Ableitung. Will man nun die Steigung einer Funktion an einer bestimmten Stelle bestimmen, muss die Funktion an dieser Stelle auch differenzierbar sein. Das ist praktisch die Voraussetzung, um überhaupt ableiten zu können.

Mit der Differenzierbarkeit von Funktionen haben wir uns im letzten Artikel genauer beschäftigt. Kurz gefasst bedeutet „differenzierbar“, dass an der Stelle x₀ (eine bestimmte Stelle, an der man die Steigung herausfinden möchte), der Grenzwert existiert. Der Grenzwert einer Funktion, auch „Limes“ (abgekürzt mit „lim“), wird mit folgender Formel ausgedrückt:

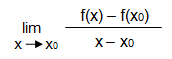
An einer gekrümmten Funktion kann man nicht (wie bei einer Geraden) einfach durch das Anlegen eines Steigungsdreiecks die exakte Steigung an einer bestimmten Stelle x₀ bestimmen. Hier versucht man, den Abstand zwischen den zwei Punkten immer kleiner werden zu lassen, so klein wie nur möglich (=Grenzwert). Man muss sich das so vorstellen, dass sich der Punkt P₁ dem Punkt P₀, bzw. die Stelle x₁ an x₀ immer weiter annähert. Irgendwann hat man keine Sekante mehr, die durch zwei Punkte (P₁ und P₀₎ läuft, sondern eine Tangente, welche die Funktionsgraphen an der Stelle x₀ berührt, bzw. tangiert.

Beim Ableiten tut man also nichts anderes, als den Grenzwert der Funktion bilden, indem man x gegen x₀ streben lässt. Dies wird durch den kleinen Pfeil unterhalb von „lim“ gekennzeichnet. Wenn wir uns die Formel zur Grenzwertbildung nochmal anschauen, wird auch deutlich, dass x niemals gleich x₀ sein kann, da ansonsten unter dem Bruch eine Null stehen würde (x_{0 –} x₀) und dieser Ausdruck nicht definiert ist.

Natürlich lässt sich der Grenzwert einer Funktion nicht nur an einer bestimmten Stelle bestimmen, sondern für jede andere Zahl x, solange sie denn innerhalb des Definitionsbereichs liegt. Ordnet man nun jedem x aus dem Definitionsbereich der Funktion f(x) eine Ableitung zu, so erhält man eine neue Funktion f'(x). Diese neue Funktion nennt man dann Ableitungsfunktion oder kurz „Ableitung von f(x)“. Die Ableitungsfunktion gibt somit zu einer beliebigen Stelle der Funktion die entsprechende Steigung an. Der errechnete Grenzwert nennt sich dann „Differentialquotient“.

Um auf unser Beispiel von vorhin zurückzukommen, hat die Funktion f(x) = 2x² an einer beliebigen Stelle x₀ die Steigung f‚(x₀) = 4x₀. Die Steigung bei x₀=0,5 wäre demnach 4*0,5=2. Die Ableitungsfunktion lautet entsprechend f'(x) = 4x. Schauen wir uns nochmal das Steigungsdreieck zur Funktion f(x) = 2x² an. Vergleicht man nun die beiden Steigungen, so stellt man fest, dass das Steigungsdreieck mit einer errechneten Steigung von 4/1 = 4 recht ungenau war. Denn die tatsächliche Steigung an der Stelle x=0,5 beträgt 2. Die Abweichung wird umso geringer, je kürzer der Abstand zwischen P₁ und P₀ wird. Und genau darum geht beim Ableiten, diesen Abstand so gering wie nur möglich werden zu lassen.

Da je nach Quelle unterschiedliche Schreibweisen für die Ableitungsfunktion verwendet werden, möchte ich hier nochmal kurz die gängigen Synonyme für f'(x) auflisten:

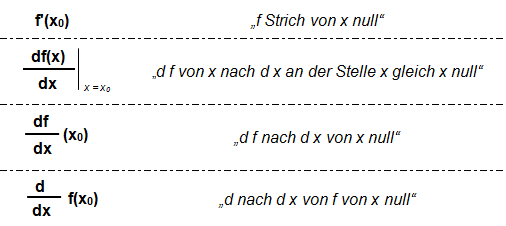
In weiteren Verlauf des Artikels wird jedoch die geläufigere Schreibweise f'(x) verwendet. Im folgenden Abschnitt schreiten wir nun intensiver zur Tat, indem wir die wichtigsten Ableitungsregeln anhand von Beispielen betrachten.

Ableitungsregeln Beispiele

In der Differentialrechnung haben wir es i.d.R. mit zusammengesetzten Funktionen zu tun, wie z.B. 2x³ – 4x +5, sin(3x) oder e^(5-x). Zum Ableiten solcher Funktionen gibt es Ableitungsregeln, mit deren Hilfe man Differenzieren kann.

Einige Regeln sind recht simpel und daher leicht zu merken, die anderen sind komplexer und müssen teilweise auswendig gelernt werden. Doch auch beim Ableiten gilt wie so häufig: „Übung macht den Meister“. Je mehr Beispielaufgaben man zu den verschiedenen Ableitungsregeln durchrechnet, umso leichter fällt es, sich die Formeln zu merken.

Im Folgenden widmen wir uns zunächst den grundlegenden Ableitungsregeln, darunter:

• Konstante Funktion
• Potenzregel
• Faktorregel
• Summenregel
• Produktregel
• Quotientenregel
• Kettenregel

Auch die Ableitungsregeln zu Logarithmusfunktionen, Exponentialfunktionen, Winkelfunktionen & Co. werden betrachtet und zusammen mit den grundlegenden Ableitungsregeln nochmal in einer Tabelle dargestellt.

Konstante Funktion ableiten

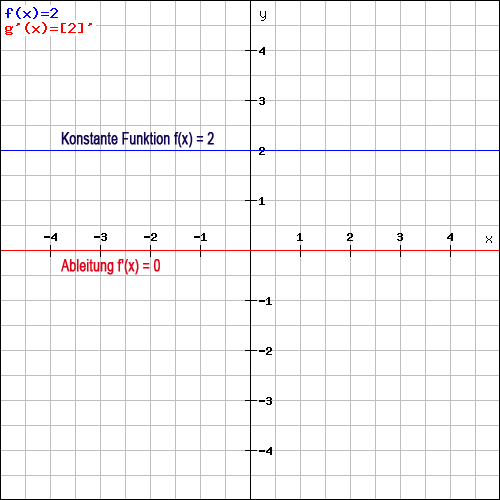
Eine konstante Funktion nimmt für alle x-Werte denselben Funktionswert an. Sie ist demnach eine parallel zur x-Achse verlaufende (“waagerechte“) Gerade. Der y-Wert bleibt dabei überall gleich. Da eine Gerade keine Steigung hat, ist die Ableitung einer konstanten Funktion immer Null.

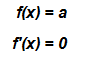
Anhand der folgenden Grafik wird es deutlich. Nehmen wir als Beispiel die konstante Funktion f(x) = 2 (blaue Gerade). Egal, welchen x-Wert man wählt, eine Steigung ist nicht vorhanden. Daher ist die Ableitungsfunktion f'(x)=0.

Ob die Funktion nun die Konstante 3, 5, -22 oder 1.745 hat ist egal. Solange es sich um eine reine Zahl (ohne x-Wert) handelt, fällt diese beim Ableiten komplett weg. Die Funktion muss daher nicht nur aus einer Konstanten bestehen, sondern kann auch f(x) = 3x + 2 lauten. Bei der Bildung der Ableitung würde hier die Zahl 2 komplett wegfallen.

Potenzregel

Die Potenzregel ist neben der Ableitung einer Konstante die wohl am häufigsten verwendete Ableitungsregel. Schließlich hat man es in der Differentialrechnung weniger mit linearen Funktionen, sonder in erster Linie mit nichtlinearen Funktionen, wie z.B. x², x³ usw. zu tun.

Die Ableitung einer Potenzfunktion wird wie folgt gebildet:

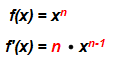
Die Potenz der Funktion (hoch 2, hoch 3 etc.) wird beim Ableiten also immer Eins weniger. Gleichzeitig wird die der Wert der Potenz mit x multipliziert.

Beispiel: f(x) = x³

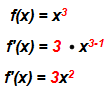
Die Ableitung der Potenzfunktion x³ ist die quadratische Funktion 3x².

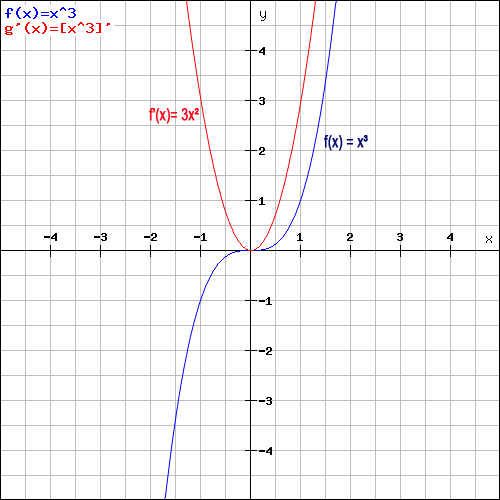
Die Ableitungsfunktion f'(x) = 3x² gibt die Steigung der Orginalfunktion f(x) =x³ an. Wie man anhand der Grafik gut erkennen kann, nimmt die Originalfunktion (blau) für alle x < 0 negative Funktionswerte und für alle x > 0 positive Funktionswerte an. Schaut man sich nun die Ableitungsfunktion (rot) an, so stellt man fest, dass diese für alle  x < 0 eine negative Steigung und für alle x > 0 eine positive Steigung annimmt. Um die Steigung der Funktion x³ an einer bestimmten Stelle x₀ herauszufinden, setzt man einfach den entsprechenden x-Wert in die Ableitungsfunktion 3x² ein.

Weitere Ableitungsbeispiele, bei denen die Potenzregel angewendet wird, sind:

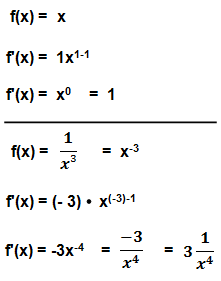
Gerade das zweite Beispiel mit dem Bruch zeigt, dass oft schon eine simple Umformung der Funktion ausreicht, um die Potenzregel anwenden zu können. Diese Umformungen sollte man daher beherrschen.

Faktorregel

Die Faktorregel findet immer dann Anwendung, wenn eine Funktion f(x) mit einer beliebigen reellen Zahl c multipliziert wird. Dies ist z.B. bei g(x) = 3x² der Fall, denn diese Funktion setzt sich aus der Zahl c= 3, multipliziert mit der Potenzfunktion f(x)=x² zusammen.

Die Faktorregel lautet:

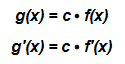
Angewendet auf unser Beispiel g(x) = 3x² lautet die Ableitung der Funktion:

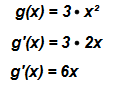
Man wendet bei x² die Potenzregel an und multipliziert das Ergebnis anschließend mit der Zahl c, also in dem Fall mit 3. Anhand der Grafik erkennt man gut, dass aus einer quadratischen Funktion per Ableitung eine lineare Funktion wird.

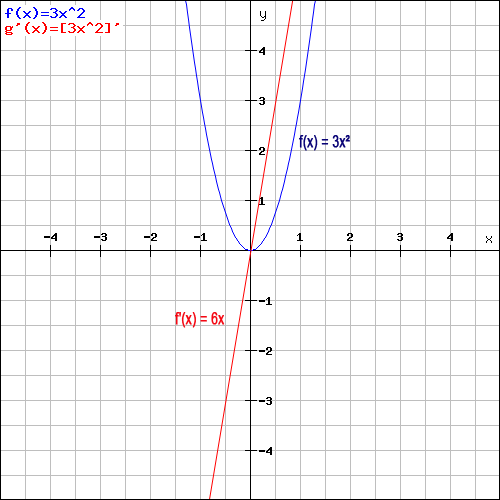
Auch hier ist anhand des roten und blauen Funktionsgraphen zu erkennen, dass die Ableitungsfunktion f'(x) überall dort negative Funktionswerte annimmt, wo die Originalfunktion f(x) eine negative Steigung hat, also bei x < 0. Bei > 0 hat die blaue Parabel eine positive Steigung, ebenso befinden sich dann auch die Funktionswerte der Geraden im positiven Bereich.

Betrachten wir nochmal ein etwas kniffliges Beispiel, bei welchem auch die Faktorregel eingesetzt wird, obwohl man es auf den ersten Blick gar nicht annimmt:

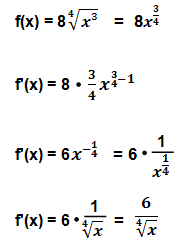
Eine Wurzel lässt sich also immer auch als Potenz schreiben, dabei wird der Term in der Wurzel zum Zähler, der Term über der Wurzel zum Nenner. Als Potenz lässt sich die Funktion dann nach der Potenzfunktion ableiten.

Wichtig: Die Faktorregel gilt nur bei Multiplikation mit c, nicht bei Addition! Würde die Funktion f(x) = 3 + x² lauten, würde die Zahl drei gemäß der Ableitungsregel für Konstanten wegfallen. Die Ableitungsfunktion wäre dann 2x.

Summenregel

Die Summenregel besagt, dass bei der Ableitung einer Funktion, die sich durch Addition und/oder Subtraktion mehrerer Funktionen zusammensetzt, gliedweise differenziert werden darf. Nehmen wir z.B. die Funktion f(x) = 5x² +3x. Diese setzt sich aus g(x) = 5x² und h(x)=3x zusammen. Die Ableitung der Funktion f(x) ist nun die Summe der Ableitungen von g(x) und h(x).

Die Summenregel lautet:

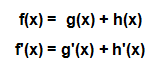
Die Ableitung von f(x) = 5x² +3x lautet demnach:

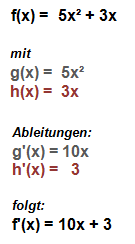
Anhand der Grafik lässt sich das errechnete Ergebnis auch schnell überprüfen. Die Parabel nimmt hier für alle x < -0,25 eine negative und für alle x > -0,25 eine positive Steigung an. Und auch die Ableitungsfunktion 10x+3 nimmt für x < -0,25 negative und für  x > -0,25 positive Funktionswerte an.

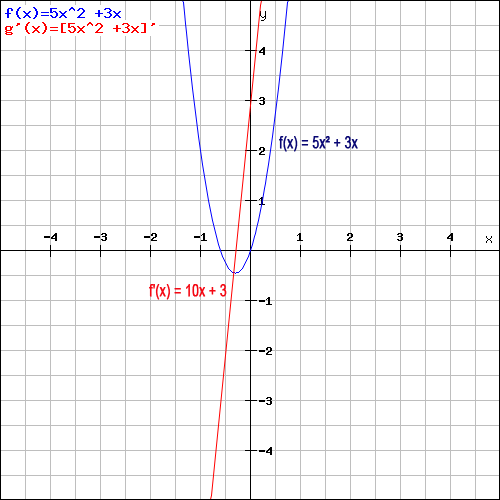
Obwohl die Summenregel dem Namen nach für Summen angewendet wird, gilt sie auch bei Subtraktion von mehreren Funktionsgliedern. Man kann sie dann auch als „Differenzenregel“ bezeichnen.

Zum Veranschaulichen kommen jetzt noch ein paar Beispiele:

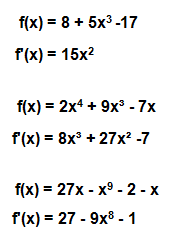
Produktregel

Bei der Summenregel haben wir die Ableitung von Summen und Differenzen behandelt. In den beiden nächsten beiden Abschnitten widmen wir uns nun dem Ableiten von Produkten und Quotienten. Schauen wir uns zunächst die Produktregel an, die bei Funktionen angewendet wird, bei welchem die Funktionsglieder durch Multiplikation miteinander verbunden sind.

Die Formel zum Ableiten von Produkten lautet:

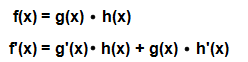
Die Formel sieht zwar auf den ersten Blick etwas kompliziert aus, ist sie aber nicht. Wichtig ist, dass man Schritt für Schritt vorgeht, dann kann auch nichts schiefgehen. Betrachten wir ein Beispiel die Funktion f(x) = 6x³ * 4x:

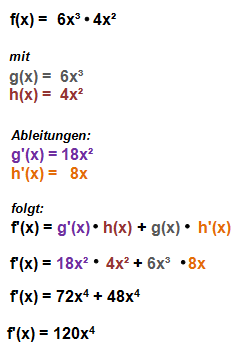
Die abgebildeten Funktionsgraphen verdeutlichen das Ergebnis. Bei x < 0 fällt die Originalfunktion und die Ableitung nimmt negative Funktionswerte an. Ist x > 0 steigt die Originalfunktion und auch die Parabel nimmt dann für alle positiven x-Werte auch positive Funktionswerte an.

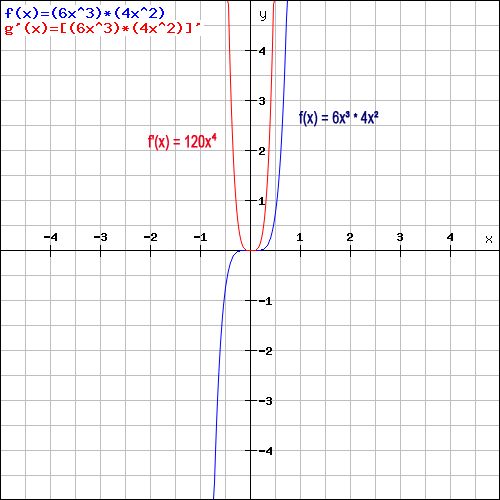
Weitere Ableitungsbeispiele zur Produktregel:

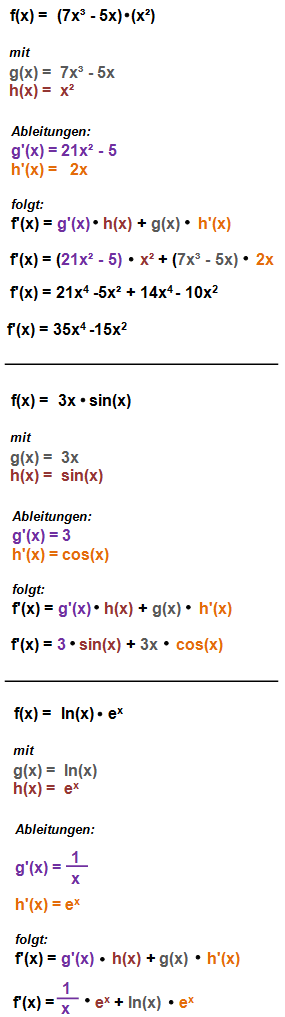
Bei den beiden letzten Beispielen mit sin(x) und ln(x) kommen spezielle Ableitungen zur Anwendung, die man einfach auswendig lernen muss. So ist z.B. die Ableitung von sin(x) gleich cos(x). Bei e^x  gibt es eine Besonderheit, denn auch die Ableitung lautet e^x. Solch wichtige Ableitungsregeln werden aber am Ende des Artikels aber nochmal übersichtlich in einer Tabelle dargestellt.

Quotientenregel

In der Differentialrechnung hat man es oftmals mit gebrochenrationalen Funktionen, also Brüchen zu tun. Um diese abzuleiten, wird die Quotientenregel angewendet. Die Quotientenregel ist neben der Kettenregel eine der komplizierteren Ableitungsregeln, aber ähnlich wie bei der Produktregel gilt: Wer schrittweise vorgeht, steht auf der sicheren Seite.

Die Quotientenregel lautet:

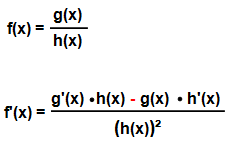
Im Zähler entspricht die Quotientenregel der Produktregel, bis auf den Unterschied, dass zwischen den Produkten ein Minuszeichen und kein Pluszeichen steht. Das Einzige, was man sich dann nur für die Ableitungsfunktion noch merken muss, ist der Nennerausdruck, nämlich das Quadrat des ursprünglichen Nenners.

Betrachten wir ein Beispiel:

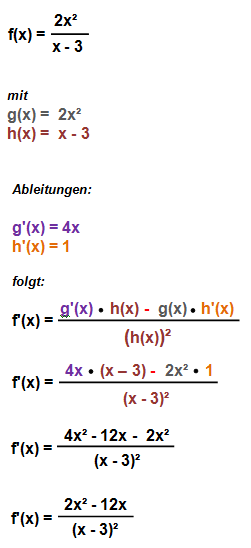
Und auch wenn die Funktionsgraphen der Original- und Ableitungsfunktion auf den ersten etwas kompliziert aussehen, so kann man auch hier gut erkennen, dass die Originalfunktion bei negativen x-Werten steigt und bei positiven x-Werten fällt. Ebenso nimmt die rote Ableitungsfuntkion bei x <0 positive Funktionswerte und bei x > 0 negative Funktionswerte an.

Weitere Funktionen, bei denen die Quotientenregel eingesetzt werden muss, wären z.B.:

Schauen wir uns nun ein Beispiel mit einer Wurzel an. Man kann für eine Wurzel auch immer x^0,5 schreiben und die Ableitung so vereinfachen.

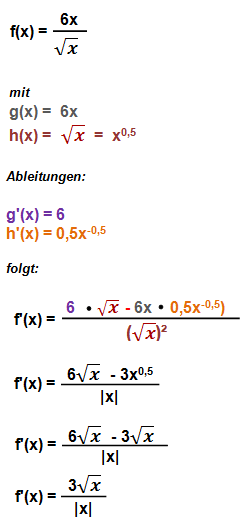
Im Nenner steht nach der Ableitung der Funktion nicht nur x, sondern der Betrag von x (|x|). Warum? Im Beispiel steht x unterhalb der Wurzel, gleichzeitig wird der Term aber auch quadriert. Daraus ergibt sich x^0,5 multipliziert mit x² = x¹, also x. Da aber x beim Quadrieren sowohl eine positive, als auch eine negative Zahl sein könnte, kommen die Betragsstriche zum Einsatz. Denn der Betrag von x ist immer unabhängig vom Vorzeichen.

Kettenregel

Kommen wir nun zur Königin der Ableitungsregeln, der Kettenregel. Sie kommt immer dann zum Einsatz, wenn mehrere Funktionen miteinander verkettet sind, d.h. wenn wir es mit Funktionen von Funktionen zu tun haben. Dies ist relativ oft der Fall, sodass die Kettenregel in der Differentialrechnung auch häufig zum Einsatz kommt.

Die Ableitung verketteter Funktionen erhält man, indem man die Ableitungen alle ineinander verschachtelten Funktionen miteinander multipliziert:

Die Funktionen g(x) und h(x) sind ineinander verschachtelt, sodass g(x) die Funktion aus h(x) ist = g(h(x)). Wir haben es hier also mit einer Funktion von einer Funktion zu tun. Man bezeichnet h(x) als „innere Funktion“ und g(x) als „äußere Funktion“.

Zur Ableitung von g(h(x)) muss man sich merken: „Innere Ableitung mal äußere Ableitung“. Die innere Ableitung wird zuerst gerechnet, die äußere Ableitung zuletzt.

Die Kettenregel lässt sich an einem Beispiel einfacher erklären:

Die entsprechende Grafik sieht etwas wirr aus, aber ähnlich wie bei den vorangegangenen Beispielen entspricht auch hier die rote Ableitungsfunktion der Steigung der Originalfunktion.

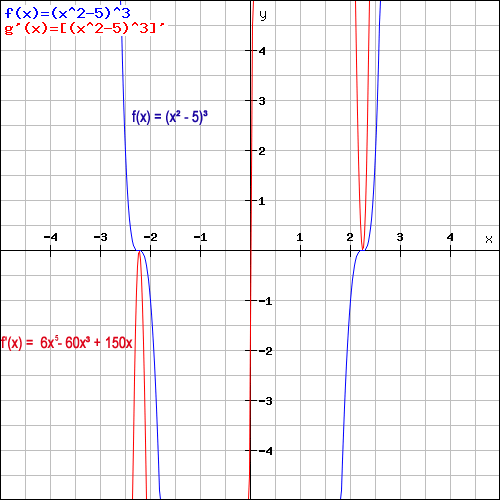
Die Schwierigkeit bei der Kettenregel ist es meist, den inneren Term h(x) von g(x) zu unterscheiden. Es gehört sicherlich etwas Übung dazu, bis man Funktionen, bei denen die Kettenregel angewendet wird, auf den ersten Blick erkennt. Voraussetzung ist jedoch immer, dass die Funktionswerte der einen Funktion, von Funktionswerten der anderen Funktion abhängen. Der innere Term einer verketteten Funktion ist dabei immer der, der mit dem x am engsten verbunden ist. Im äußeren Term darf das x dann nicht mehr auftauchen.

Schauen wir uns noch ein paar typische Beispiele zur Kettenregel an:

Das Entscheidende bei der Kettenregel, aber auch bei der Potenz- und Quotientenregel ist es, zu erkennen, welche Ableitungsregel angewendet werden muss. Daher ist es wichtig, sich die Funktion genau anzuschauen. Handelt es sich um ein Produkt, einen Quotienten oder kommt beides darin vor? Handelt es sich um eine einfache oder eine verkettete Funktion? Denn oft hat man es auch mit Aufgaben zu tun, in denen Kettenregel und/oder Potenzregel, sowie Quotientenregel zur Anwendung kommen.

Auch gibt es Beispiele, in denen die Kettenregel gleich zweimal zur Anwendung kommt, wie im folgenden Fall:

Und wer immer noch nicht genug hat, findet hier weitere Beispiele zur Kettenregel und ein komplizierteres Beispiel zur Kettenregel mit Bruch und Wurzel.

Tipps zum Ableiten von Funktionen

Beim Ableiten gilt es zwei Dinge zu beachten: Zum Einen sind die grundlegenden mathematischen Kenntnisse unerlässlich. Ob binomische Formeln, Potenzgesetze, Rechnen mit Brüchen und Wurzeln etc. – Wenn man nicht weiß, wie man welche Gleichung umformen kann, wird es auch mit der Ableitung nichts. Es gilt somit ggf. Grundkenntnisse aufzufrischen. Hier kann ich z.B. das Online-Tutorial „Grundlagen Mathematik“ von Lecturio empfehlen, bei dem die ganzen Basics Schritt für Schritt mit zahlreichen Beispielaufgaben aufgearbeitet werden.

Zum Anderen sollte man die wichtigsten Ableitungsregeln kennen und idealerweise auswendig zu können. Diese sind in der folgenden Tabelle dargestellt und können auf als PDF heruntergeladen werden.

Wichtige Ableitungsregeln

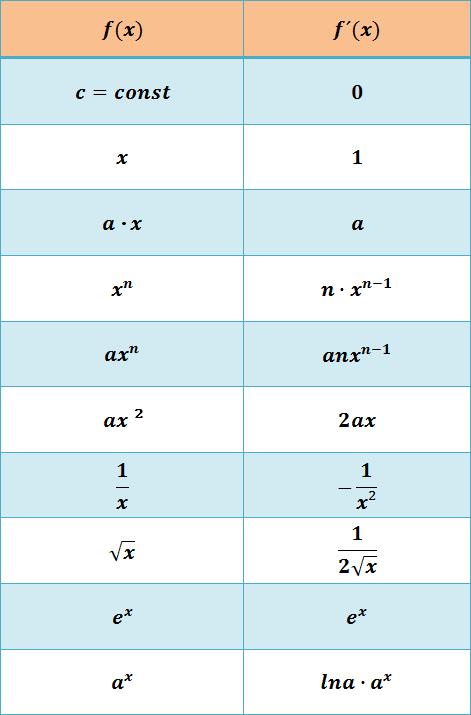
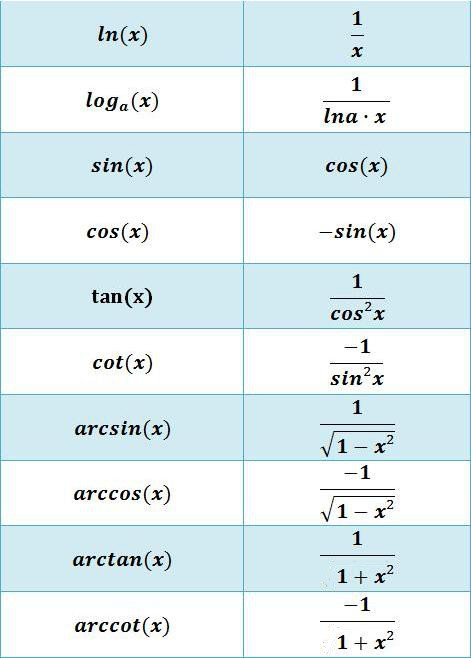
Diese Ableitungsregeln können zusammen mit den betrachteten Ableitungsregeln für verknüpfte Funktionen hier als PDF heruntergeladen werden.

Erste Ableitung, zweite Ableitung, dritte Ableitung usw.

In den betrachteten Beispielen haben wir die 1. Ableitung einer Funktion, also die Ableitungsfunktion f'(x) betrachtet. Diese Ableitungsfunktion kann man natürlich wieder ableiten und erhält dann die 2. Ableitung von f(x). Die 2. Ableitungsfunktion ist dann mit zwei Strichen gekennzeichnet: f“(x). Theoretisch ließe auch diese sich wieder ableiten und man würde dann die 3. Ableitung f“'(x) erhalten usw. Das geht natürlich nur solange, bis überhaupt noch etwas zu differenzieren ist. Aber die berechtigte Frage lautet ja: Wozu dazu Ganze?

Ich habe jeweils in dem ersten Beispiel der jeweiligen Ableitungsregel eine Grafik mit den Funktionsgraphen der Funktion f(x) und der 1. Ableitung f'(x) ergänzt. Bei genauerer Betrachtung lässt sich zwischen den beiden Funktionen bereits ein Zusammenhang herstellen.

Schauen wir uns hierzu nochmal ein Beispiel ein, nämlich die Funktion x³+2x²-2x-2. In der folgenden Grafik sind die Funktionsgraphen der Originalfunktion (blau), der 1. Ableitung (rot) und der zweiten Ableitung (grün) eingezeichnet.

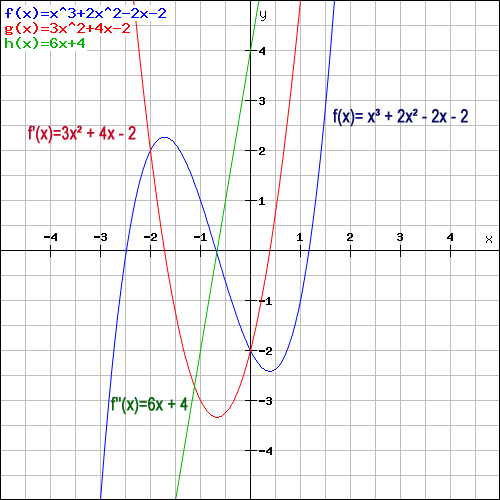
Wie eingangs bereits erwähnt, gibt die Abbleitung einer Funktion ihre Steigung an einer beliebigen Stelle x₀ an. Die 1. Ableitung (rot) gibt somit Aufschluss über die Steigung der Originalfunktion (blau). Dort, wo der Funktionsgraph f(x) fällt, hat auch die rote Parabel einen negativen Verlauf. Ebenso verhält es sich mit der 2. Ableitung (grüne Gerade). Diese ist die Ableitung der 1. Ableitung und hat dort, wo die rote Parabel steigt, positive Funktionswerte, dort wo sie abfällt, negative Funktionswerte.

Doch neben der Steigung gibt es noch weitere Zusammenhänge zwischen Originalfunktion, 1. Ableitung und 2.Ableitung. Es fällt z.B. auf, dass die Originalfunktion dort, wo sich die Nullstellen der 1. Ableitung befinden, einen Hoch- und Tiefpunkt hat. Und an der Stelle, wo die 1. Ableitung (rot) ihren Extremwert, bzw. Tiefpunkt hat, befindet sich die Wendestelle der Originalfunktion (blau).

Und auch bei der 2. Ableitung lassen sich Zusammenhänge feststellen. So gibt die Nullstelle der 2. Ableitungsfunktion Aufschluss über den Tiefpunkt der 1. Ableitung und gleichzeitig auch über die Wendestelle der Originalfunktion.

Da man bei dem ganzen Wirrwarr schnell den Überblick verlieren kann, gibt es eine kleine Merkhilfe. Dabei schreibt man die einzelnen (Ableitungs-)Funktionen f, f ‚, f “ etc. untereinander und daneben in versetzt das Wort NEW:

f …….. . N . E . W
f ‚ …………..N . E. W
f “ ………………N. E. W
…

Die Buchstaben, die untereinander stehen, entsprechen sich jeweils. So ist z.B. die Nullstelle der 2. Ableitung f “ gleichzeitig die Extremstelle der 1. Ableitung f ‚ und die Wendestelle der Originalfunktion.

Die einzelnen Ableitungen sind somit äußerst hilfreich, um die Eigenschaften und charakteristischen Merkmale von Funktionen zu bestimmen. Diese werden in den nächsten beiden Artikeln zu Funktionsuntersuchungen und Kurvendiskussion noch intensiv behandelt.

Fazit

Neben dem Beherrschen von mathematischen Grundlagen, sowie den wichtigsten Ableitungsregeln ist es beim Differenzieren wichtig, sich die Funktion genau anzuschauen und von keiner noch so komplizierten Darstellung verschrecken zu lassen. Was zunächst noch kompliziert aussieht, lässt sich oft mit wenigen simplen Umformungen vereinfachen.

Sicher beim Ableiten wird man jedoch nur durch Übung. Es gibt zahlreiche Ableitungsbeispiele – Die Einen einfacher, die Anderen schwerer Natur. Sicher beim Einsatz der diversen Ableitungsregen wird man nur durch Routine. Übung macht wie so oft, auch beim Ableiten den Meister ;).

Lerntipp:

Online-Tutorials mit zahlreichen ausführlichen Ableitungsbeispielen:

• Übungsaufgaben zu Ableitungsregeln 1
• Übungsaufgaben zu Ableitungsregeln 2
• Übungsaufgaben zu Ableitungsregeln 3